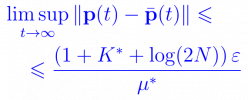В статье «Об оценках скорости сходимости для некоторых моделей массового обслуживания с неполно заданными интенсивностями», Информатика и ее применения. 2019. Т. 13. № 3, 14‒19 (авторы А. И. Зейфман, Я. А. Сатин, К. М. Киселева), получены скорости сходимости нестационарных систем обслуживания $M_t/M_t/S/S$ и $M_t/M_t/S$ в ситуации, когда заданы интегралы по периоду от интенсивностей поступления и обслуживания требований.
Число требований в системе при этом описывается неоднородным процессом рождения и гибели с конечным пространством состояний $\{0,1,\dots,S\}$ в первом случае, и счетным пространством состояний $\{0,1,\dots,\}$ – во втором. Требования поступают и обслуживаются по одному, интенсивность поступления требования в момент $t$ равна $\lambda_k(t)=\lambda(t)$. Интенсивность обслуживания требования, если длина очереди в текущий момент равна $k$, есть $\mu_k(t)=k\mu(t)$ для первой модели, и $\mu_k(t)=\mu(t)\min(k,S)$ для второй модели.
При этом интенсивности поступления $\lambda(t)$ и обслуживания требований $\mu(t)$ являются 1-периодическими функциями времени и известны не сами эти функции, а их «средние» значения то есть числа $\lambda^*=\int_0^1\lambda(t)\, dt$ и $\mu^*=\int_0^1\mu (t)\, dt$.
Для построения вероятностных характеристик моделей была написана программа для СМО $M_t/M_t/S/n$, с помощью которой можно исследовать обе рассматриваемые в статье ситуации: $M_t/M_t/S$ и $M_t/M_t/S/S$.
При этом пользователь может задавать следующие параметры системы
- максимальное число требований в системе $n$;
- число серверов $s$;
- интенсивности поступления и обслуживания;
- состояния, вероятности которых надо построить;
- время $t$, оценив его предварительно или исходя из каких-то других соображений.
Ниже представлен ролик, показывающий способ построения