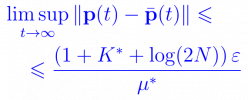Рассматриваемый подход базируется на исследовании прямой системы дифференциальных уравнений Колмогорова для рассматриваемого процесса $X(t)$. Можно выделить следующие основные этапы:
- получение верхних оценок скорости сходимости, то есть, грубо говоря, нахождение момента времени, скажем $t^*$ такого, что начиная с него вероятностные характеристики $X(t)$ с заданной погрешностью не зависят от начальных условий;
- получение аналогичных нижних оценок, наличие которых гарантирует, что «независимость» от начальных условий не может достигаться раньше некоторого момента $t_*$;
- получение оценок устойчивости («perturbation bounds») для возмущенного процесса с близкими инфинитезимальными характеристиками;
- в случае большой размерности исходного процесса (или счетного числа состояний) аппроксимации с помощью процессов меньшей размерности.
В итоге, если изучается модель с 1-периодическими по времени интенсивностями, то имея все эти оценки, мы далее решаем прямую систему Колмогорова с простейшим начальным условием $X(0)=0$ для усеченной системы на отрезке $[0, t^*+1]$. А тогда на отрезке $[t^*,t^*+1]$, получаем с требуемой погрешностью основные предельные характеристики как самого процесса $X(t)$, так и близких «возмущенных» процессов. При этом, как известно, важнейшим является пункт а), на котором основано получение оценок устойчивости и погрешности усечения.