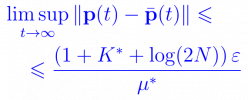Нестационарные модели систем обслуживания типа $M^X_n/ M^X_n/1$ — Количественные методы исследования марковских цепей и моделей, и их приложения

Применение метода дифференциальных неравенств к оценке скорости сходимости одного класса цепей Маркова

В статье «Application Method of Differential Inequalities to Bounding the Rate of Convergence for a Class of Markov Chains» (Применение метода дифференциальных неравенств к оценке скорости сходимости одного класса цепей Маркова), Springer Series in Mathematics & Statistics, vol. 333, P. 95-103, doi:10.1007/978-3-030-56323-3_8 (авторы А. Л. Крюкова, В. С. Ошушкова, А. И. Зейфман, Я. А. Сатин) рассматривается класс марковских систем обслуживания, в котором требования поступают все одновременно и обслуживаются по одному. В этом случае метод логарифмической нормы не позволял получить точную оценку скорости сходимости системы к предельному режиму. Поэтому для получения решения этой задачи авторами предложен альтернативный способ исследования – метод дифференциальных неравенств.

В статье рассмотрена также соответствующая нестационарная модель с 1-периодическими интенсивностями поступления и обработки требований. На основании полученной оценки скорости сходимости вычислены предельные характеристики. Приведен численный пример, который показывает практическую применимость изложенного подхода.

Два подхода к построению оценок устойчивости для нестационарных марковских цепей

В статье «Two Approaches to the Construction of Perturbation Bounds for Continuous-Time Markov Chains» (Два подхода к построению оценок устойчивости для нестационарных марковских цепей), Mathematics 2020, 8, 253; doi:10.3390/math8020253 (авторы А. И. Зейфман, В. Ю. Королев, Я. А. Сатин), рассмотрены два общих подхода для построения оценок устойчивости предельных характеристик неоднородных марковских цепей с непрерывным временем по отношению к возмущениям их инфинитезимальных характеристик. Рассмотрено получение такого рода оценок для процесса, описывающего число требований в системе обслуживания $M(t)^X_n/M(t)^X_n/1$ с возможным групповым поступлением и/или обслуживанием требований, а также системе с катастрофами. В качестве примеров изучены конкретные модели типа $M_t/M_t/N/N$ и $M_t^X/M_t/2$, причем во второй модели предполагается, что требования поступают не более чем по два одновременно.

On three methods for bounding the rate of convergence for some continuous–time Markov chains

В статье «On Three Methods for Bounding the Rate of Convergence for Some Continuous–Time Markov Chains» (авторы А. И. Зейфман, Я. А. Сатин, А. Л. Крюкова, Р.В. Разумчик, К.М. Киселева, Г.Н. Шилова) рассматриваются три различных подхода для получения оценок скорости сходимости к предельному режиму для различных неоднородных марковских цепей с непрерывным временем. В частности, такие цепи можно рассматривать как число требований в нестационарной системе обслуживания типа $M^X_n/M^X_n /1$. Первый подход к получению оценок основан на логарифмической норме, второй на функции Ляпунова, и третий на методе неравенств. В статье приведены два численных примера, которые показывают практическую применимость изложенных подходов.

Об оценках скорости сходимости и предельных характеристиках для нестационарной модели массового обслуживания

В статье «On the Rate of Convergence and Limiting Characteristics for a Nonstationary Queueing Model» (Об оценках скорости сходимости и предельных характеристиках для нестационарной модели массового обслуживания), Mathematics 2019, 7, 678; doi:10.3390/math7080678 (авторы А. И. Зейфман, Я. А. Сатин, А. Л. Крюкова), получены скорости сходимости для аналога нестационарной системы обслуживания $M_t/M_t/1$ в ситуации, когда требования поступают, как обычно, поодиночке, но обслуживаются только парами.

Об оценках скорости сходимости для некоторых моделей массового обслуживания с неполно заданными интенсивностями

В статье «Об оценках скорости сходимости для некоторых моделей массового обслуживания с неполно заданными интенсивностями», Информатика и ее применения. 2019. Т. 13. № 3, 14‒19 (авторы А. И. Зейфман, Я. А. Сатин, К. М. Киселева), получены скорости сходимости нестационарных систем обслуживания $M_t/M_t/S/S$ и $M_t/M_t/S$ в ситуации, когда заданы интегралы по периоду от интенсивностей поступления и обслуживания требований.